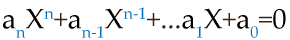| Input | Output |
|---|
Unit Conversion: Length
Constants
Equation Solver
Scientific calculator
At times, calculations are not as simple as adding or subtracting two numbers. For example, if you have to determine the value for Sin 60, a proper scientific calculator would be required for it. It is not that easy to get hold of a quality scientific calculator which can be used online and does not carry accuracy problems. Our tool is dependable and no accuracy issues are present. It is a free option and users can use it without installations.
Get correct results with a hassle free procedure
Working with geometrical formulae can be problematic at times. If you are dealing with triangles, you would be dealing with Sin, Cos and Tan. These are three commonly used formulae to determine the values of angles. It is quite hard to determine the correct values without having a high standard scientific calculator. With this tool, you can afford to stay tension free even while performing the most complex calculations. When the input values have been entered, the user does not have to perform any other task.
Developing an understanding of the usage process
The usage process of a tool is an important parameter. It is not a good alternative to finalize a tool. The following steps are used to use this tool. As compared to a lot of other tools, it has a simple procedure.
- Which input values have to be entered?
The input values depend on the calculation which you wish to perform. We can go through an example and gain more understanding. Consider that you want to determine the value of Tan 45. Simply click the “Tan” button and enter the value (45 in this case) and then close the parenthesis. To produce the output, simply click the “equal button” and results would be produced.
- Viewing the details of the outputs
When you click the “equal button”, the result would be shown under the History tab on the right. In the above example, we have to determine the value of Tan 45. When the inputs will be entered, 1.62 (value of Tan 45) will be displayed on the right side of the screen.
Other features
- One of the features of this tool is unit conversion. To start with, click the “unit conversion” tab. When you enter the value for any one of the unit, the converted form for the other units would be shown to you. For instance, if you enter the value 22 in centimeters, all the other converted units would be shown to you. This is a good feature for people who want to convert values from one unit to the other. All you need to do is enter the value in one unit. The values in all other corresponding units would be shown on your screen.
- This tool also offers the option to show the conversions between Hex, Dec and binary formats. Along with that, you can also use it to solve algebraic equations. In an overall manner, this tool works well if you want to solve complex mathematical problems.